Последовательное соединение сопротивлений (резисторов)
Если несколько резисторов (или приемников энергии) соединены один за другим без разветвлений (рис. 1) и по ним проходит один и тот же ток, то они образуют одну ветвь, такое соединение резисторов называется последовательным.
R = R1+R2+R3…+Rn; (1)
U = U1+U2+U3…+Un; (2)
I = I1 = I2 = I3 = In; (3)
P = P1 + P2 +P3…+Pn; (4)
Доказательство
Согласно закону Ома напряжения на резисторах или падения напряжения определяются выражениями
U1 = I*R1; U2 = I*R2; U3 = I*R3; U4 = I*R4;
Таким образом, падения напряжения на последовательно соединенных резисторах пропорциональны значениям их сопротивлений.
Так же мы знаем что при последовательном соединении напряжение на всём участке цепи равно сумме падения напряжения на каждом элементе последовательной цепи.
U = U1+U2+U3…+Un; (2)
Ряд последовательно соединенных резисторов можно заменить эквивалентным (общим) сопротивлением R, причем так, чтобы эта замена при неизменном напряжении на выводах соединения не вызвала изменения тока в цепи. Разделив на ток правую и левую части уравнения (2), получим
откуда следует, что эквивалентное сопротивление ряда последовательно соединенных резисторов равно сумме их сопротивлений.
Из предыдущего выражения, умножая его на I², находим, что
R1*I² + R2*I² +R3*I² +Rn*I² = R*I²;
P1 + P2 + P3 + Pn = P ;
т. е мощность, развиваемая в эквивалентном резисторе, равна сумме мощностей всех резисторов. При последовательном соединении резисторов ток в них один и тот же, поэтому мощности, развиваемые в отдельных участках (P = R*I²), пропорциональны их сопротивлениям.
Примеры задач (с решением) на последовательное соединение сопротивлений.
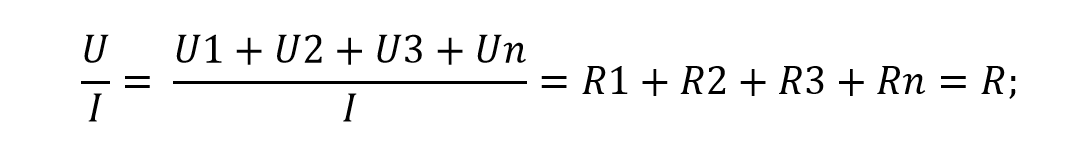
Добавить комментарий